Saphyra 2025 Spring Report
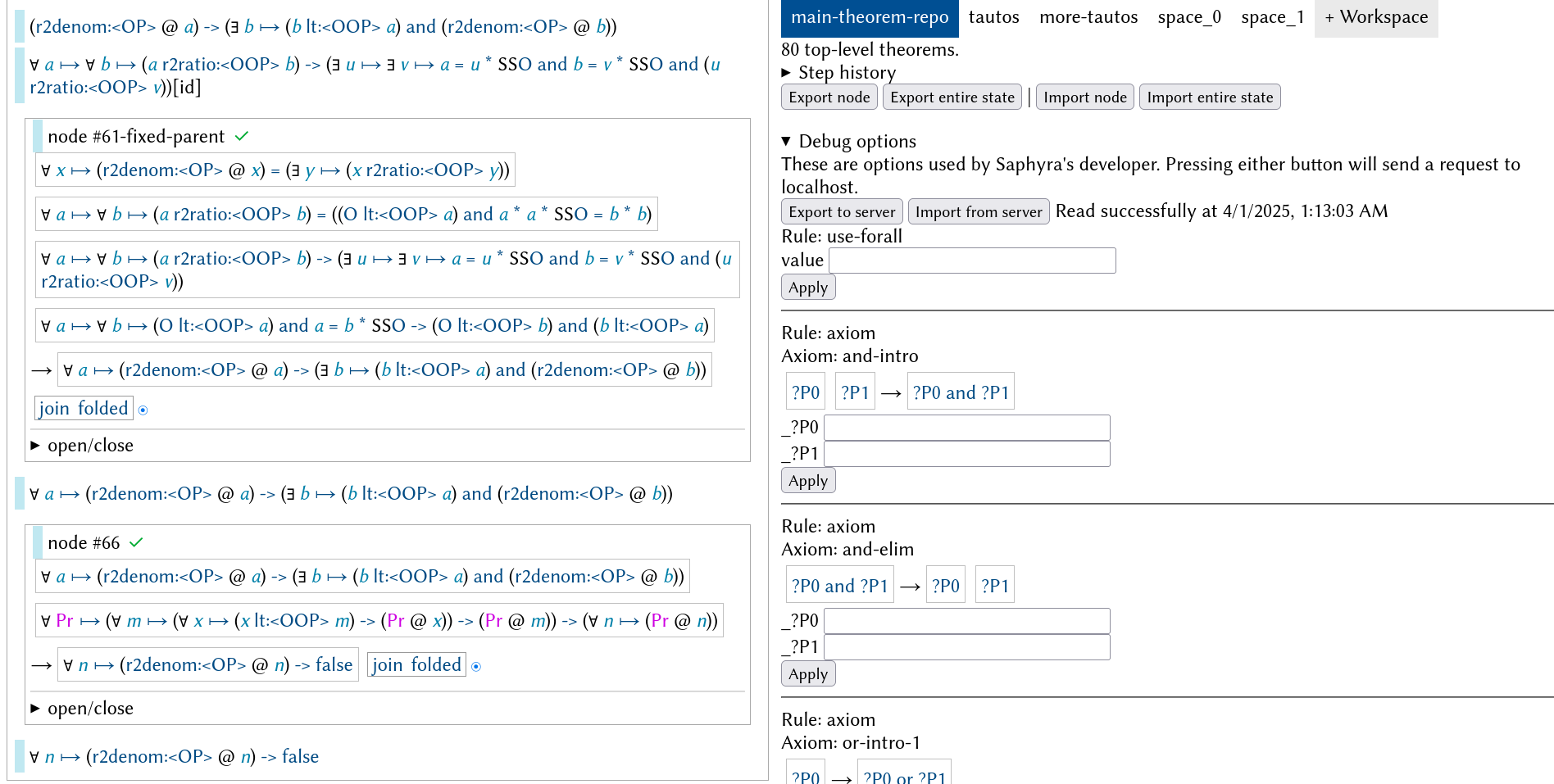
On April 1, 2025, the following theorem was successfully formalized in Saphyra:
✅ √2 is irrational
Which brings the percentage of Prof. Wiedijk's 100 theorems formalized in Saphyra to:
This is an important milestone for Saphyra: I consider it to be the first nontrivial theorem, one that requires significantly more organization and care than basic theorems (such as the associativity of +). I have bumped the version to v0.3.0 after the addition of this proof.
The theorem and its proof can be viewed on Saphyra Web as the statement: ∀ n ↦ (r2denom:<OP> @ n) -> false which can be read as “no natural number can be a denominator of √2”.
Please allow a few seconds for the proof repository to load. The theorem can be found at the bottom of the page (on the left side). Click on a “open/close” button to see details of a part of the proof.
What's new
From v0.2.0 to v0.3.0, a lot of new features were added. All of them are crucial for a fully-featured proof assistant, and most of them are crucial for the proof of “√2 is irrational”.
- Definitions.
- New definitions are made using defining statements, such as
∀ a ↦ ∀ b ↦ (a le:<OOP> b) = (∃ t ↦ a + t = b), which defines thele:<OOP>symbol, for the “less than or equal” relation (≤). - Each definition node has an extra out-link, simply labelled like
def @ le:<OOP>. This link is required when making a new definition dependent on the first one (such as defininglt:<OOP>usingle:<OOP>), which prevents circular definitions.
- New definitions are made using defining statements, such as
- Focusing.
- Instead of showing the entire proof repository, the user can now focus on a single part of the proof by clicking on the fish-eye button — ◉ — which hides the rest of the repository.
- Speedups.
- Some caching is added to speed up the verification and saving processes.
All of this made the trip to the first nontrivial theorem much easier.
What's next
Although the first nontrivial theorem is now proven, a lot of things are still missing.
- A node editor can be tremendously beneficial: it would allow better organization, easier understanding, and freer development.
- The syntax can be updated to reduce visual noise.
- More automation, such as a tactic for polynomials, will reduce a lot of manual work.
- Modular structure: allow proof modules to depend on one another.
- More lemmas: such as those regarding divisibility and primes.
- More theorems: aim to keep growing.
This is the largest and most fun personal project I have made, and I'd love to see how far I can go.